CURVA CIRCULAR SIMPLE

  Las curvas horizontales simples son arcos de circunferencia de un solo radio que unen dos tangentes consecutivas, conformando la proyección de las curvas reales o especiales, por lo tanto, las curvas del espacio no necesariamente son circulares. 

ELEMENTOS GEOMÉTRICOS QUE CARACTERIZAN UNA CURVA CIRCULAR SIMPLE

PI: punto de intersección de las tangentes o vértice de la curva.

PC: principio de la curva: punto donde termina la tangente de entrada y empieza la curva

PT: principio de tangente: punto donde termina la curva y empieza la tangente de salida 

O:  centro de la curva circular 

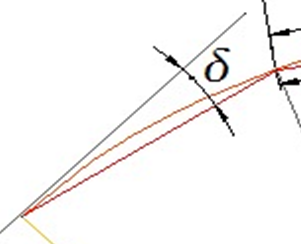
^: angulo de deflexiones  de las tangentes: angulo de deflexion principal. es igual al angulo central subtendido por PC.PT

Radio [R]: El de la circunferencia que describe el arco de la curva

Tangente [T]: Distancia desde el punto de intersección de las tangentes (PI) -los alineamientos rectos también se conocen con el nombre de tangentes, si se trata del tramo recto que queda entre dos curvas se le llama entretangencia– hasta cualquiera de los puntos de tangencia de la curva (PC o PT).

Longitud de la curva [L]: Distancia desde el PC hasta el PT recorriendo el arco de la curva, o bien, una poligonal abierta formada por una sucesión de cuerdas rectas de una longitud relativamente corta. 

Cuerda larga [CL]: Línea recta que une al punto de tangencia donde comienza la curva (PC) y al punto de tangencia donde termina (PT)

Externa [E]: Distancia desde el PI al punto medio de la curva sobre el arco.


Ordenada Media [M] (o flecha [F]): Distancia desde el punto medio de la curva hasta el punto medio de la cuerda larga.


EJEMPLO 

Para una curva circular simple, se tienen los siguientes elementos:
-Rumbo de la tangente de entrada: N76°20'E
-Rumbo de la tangente de salida: N19° 40'E


 





























  




SOLUCIÓN DEL EJERCICIO 






















1. 





1.2 


1.3


1.4

1.5


1.6

1.7


1.8

1.9




HALLAR ABSCISA PC 

HALLAR LA ABSCISA PT

















































1.

2.

2.1




3.



4.





5.

6.




































































































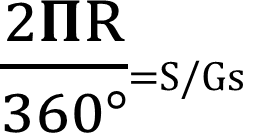
Comentarios

Publicar un comentario

Entradas más populares de este blog

CURVA CIRCULAR COMPUESTA

Imagen
 Las curvas circulares compuestas son aquellas que están  formadas por dos o mas curvas circulares simples. A pesar de que no son muy comunes, se pueden emplear en terrenos montañosos, cuando se quiere que la carretera quede lo mas ajustada posible a la forma del terreno o topografía natural, lo cual reduce el movimiento de tierras. También se pueden utilizar cuando existen limitaciones de libertad de diseño, como por ejemplo, en los accesos a puentes, en los pasos de desnivel y en las intersecciones. PI= punto de intercesión de las tangentes PC= principio de la curva compuesta PT= fin de la curva compuesta o principio de la tangente  PCC= punto común de curvas o punto de curvatura compuesta. punto donde termina la primera curva circular simple y empieza la segunda R1= radio de la curva de menor curvatura o mayor radio R2= radio de la curva de mayor curvatura o menor radio O1= centro de la curva de mayor radio O2=centro de la curva de menor radio  = angulo deflexión ...
Leer más

PATOLOGÍA DE LOS PAVIMENTO

Imagen
PATOLOGIAS  Se suele producir por una combinación de baja resistencia o capacidad de deformarse a esfuerzos de tracción de la mezcla bituminosa de la capa de rodadura y por la aparición de esfuerzos de tracción en la superficie del firme. la falta de resistencia a tracción o la excesiva rigidez de la mezcla bituminosa pueden producirse diferentes tipos de patologías ya sean físicas o químicas. TIPOS DE PAVIMENTOS. PAVIMENTO FLEXIBLE  PAVIMENTO RIGUIDO PAVIMENTO ARTICULADO TIPOS DE PAVIMENTOS PAVIMENTO FLEXIBLE En general, están constituidos por una capa delgada de mezcla asfáltica construida sobre una capa de base y una capa de subbase las que usualmente son de material granular. estas capas descansan en una capa de suelo compactado, llamada subrasante . PAVIMENTO RIGIDO Los pavimentos rígidos se integran por una capa (losa) de concreto de cemento portland que se apoya en una capa de base, constituida por grava; esta capa descansa en una capa de suelo compactado, llamada subra...
Leer más